New
Quantum Loopover
A fork of Melinda Green's Quantum loopover puzzle.
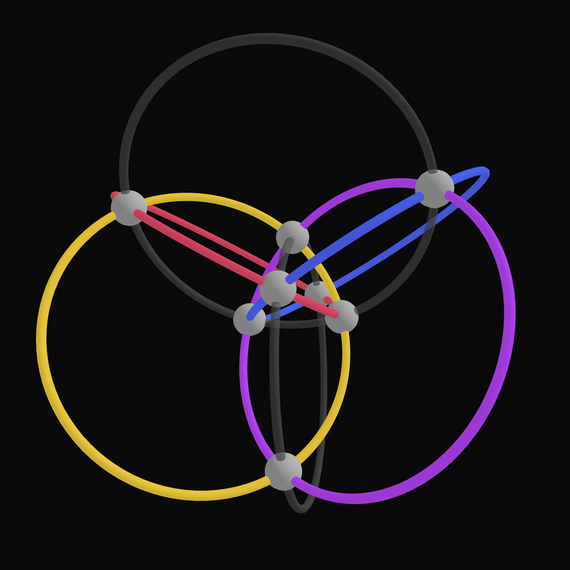
Lights Out 3D
A puzzle similar to Lights Out in spirit but based on polyhedra. Touch friendly!
Regular Star Polytopes
Visualization of regular star polytopes in 2D, 3D, 4D, and hyperbolic plane.
Models
Blast-hedra
A series of coordinate-motion puzzles.
12 x 12
Twelve interlocking dodecahedra made by straws and paper clips.
Pencil Models
Models with icosahedral symmetry.
Archive
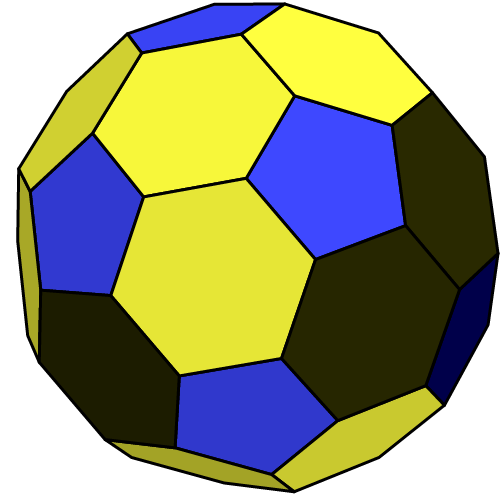
Lollipop
A 2D puzzle that contains all possible pieces twisted by all subsets of axes.
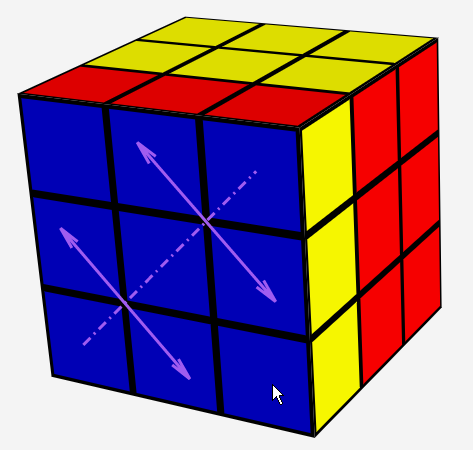
RefleCube
A Magic Cube allowing only reflection moves rather than twisting moves, or both.
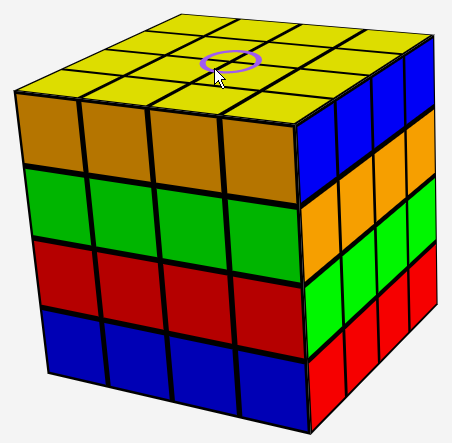
Clockwork Cube
A Magic Cube on which the rotation of all the slices are correlated.
About
I'm Nan Ma. I go by "schuma" on forums, after Michael Schumacher. I'm passionate about Twisty Puzzles, which are puzzles similar to the Rubik's Cube. You can find me on the Twistypuzzles forum. My achievements include:
- Completing all puzzles on gelatinbrain's Permutation Puzzles (see scoreboard)
- Solving 4D puzzles: MC4D tessaract, 120-cell, 24-cell, and a simplified 600-cell in Magic Puzzle Ultimate
- Mastering puzzles up to 7 dimensions
- Solving puzzles in non-Euclidean spaces (hyperbolic space, projective plane, Klein bottle) using MagicTile
- Completing the Complex 3x3x3, a sophisticated Rubik's Cube variant
I developed a tool for the Tchisla calculator game to explore optimal solutions.
In 2018, I collaborated with Roice Nelson on non-associative "twisty" puzzles, creating a proof-of-concept using integral octonions. See the introduction and source code.
Legacy
The puzzles and visualization below were built many years ago using Java Applet. Unfortunately, it's not supported by modern browsers. As of Sept 2019, I am able to start them using IE and setting http://nan.ma as a trusted website in the Java config. I don't have a plan to migrate them to new technology.
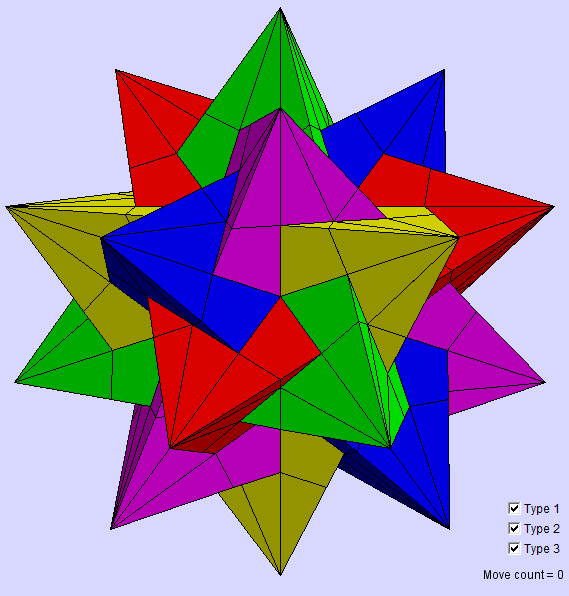
Twisty Star
A puzzle based on the beautiful compound of five tetrahedra. It is related to the face-turning icosahedra.
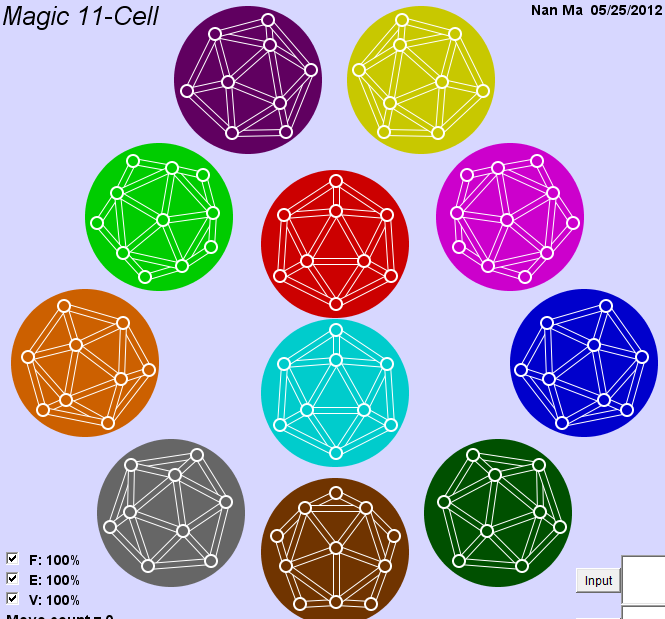
Magic 11-cell
A puzzle based on the abstract regular polytope 11-cell.
Inside H3
Not really a puzzle. It's a visualization tool to simulate what you will see when navigating a spaceship in hyperbolic polytopes.